מתמטיקה תיכונית/חשבון דיפרנציאלי/אסימפטוטות/אסימפטוטות המאונכות לציר X: הבדלים בין גרסאות בדף
imported>CommonsDelinker Replacing Asymp1.gif with File:Asymp1.png (by CommonsDelinker because: file renamed, redirect linked from other project). |
(אין הבדלים)
|
גרסה אחרונה מ־11:53, 19 ביוני 2020
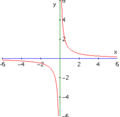
אסימפטוטה אנכית
לדוגמה, אסימפטוטות האנכיות של פונקצית השורש הם כל אותם ערכים המאפסים המכנה בלבד (). נשם לב כי ערכי הפונקציה יעברו בנקודות .
הוכחה

נתבונן בפונקציה: .
תחום ההגדרה של הפונקציה הוא: ולכן האסימפטוטה שלה עוברת ב- . באזור זה הפונקציה אינה מוגדרת אבל היא שואפת להיות במרחק הקטן ביותר ממנו.
בחקירת התנהגות הפונקציה באמצעות הצבת נקודות בגרף על פי טבלה בה מוצבים ערכי ה- הקרובים ביותר לאסימפטוטה ניתן לראות כי הפונקציה מנסה להיות ממש קרובה לאסימפטוטה.
תיאור גרפי
ניתן לשרטט אסימפטוטות מאונכות לציר בשתי אופניים
איך נדע?
בדרך כלל הנתונים של החקירה מספיקים בכדי לדעת. עם זאת, השיטה הנוחה ביותר למסתבכים היא להוסיף לטבלת נקודות הקיצון גם את ערכי האסימפטוטות. כרגיל, בין נקודות אלו נוסיף ערכים נוספים, אחד מכל צד. עבור כל ערך נבדוק האם נגזרת הפונקציה היא חיובית או שלילית:
- אם הנגזרת חיובית - הפונקציה עולה.
- אם הנגזרת שלילית – הפונקציה יורדת.
חור (נקודת אי רציפות סליקה)
בדומה לאסימפטוטה של פונקציה רציונאלית, החור מאפס את המכנה אולם הוא מאפס גם את המונה. עם זאת, מאחר שלא תמיד קל לבצע פעולה זו מומלץ לבנות תמיד טבלה.
תיאור גרפי של חור: הבדל בין אסימפטוטה לחור
-
אסימפטוטה
-
חור - נקודה ספציפית בה הפונקציה לא מוגדרת.
כאשר יש חור, הפונקציה לא מוגדרת בו. לעומת זאת אסימפטוטה ניתן לדמות לסוג של "ישר" אליו הפונקציה תמיד תשאף להיצמד..
בדיקה נקודה חשודה
- צמצום הפונקציה כמה שניתן ובדיקה האם המכנה והמונה מתאפסים. אם רק המכנה מתאפס סימן שמדובר באסימפטוטה.
- אם המכנה והמונה מתאפסים יש לנו נקודה חשודה שיכולה להיות אסימפטוטה או חור. נבדוק היכן נמצא הנעלם מסדר הגבוהה ביותר במונה או במכנה. אם הוא במכנה זוהי אסימפטוטה. אם לא במונה זוהי נקודה סליקה. ראה דוגמה, כאן
- אפשרות נוספת היא לבנות טבלה כאשר יש קושי לדעת:
- אם יש לנו ערך המאפס את המכנה לאחר צמצום תמיד נבנה טבלה ונבחן האם מדובר בחור או באסימפטוטה:
- בטבלה יהיו שבעה ערכים כשהמרכזי הוא ערך הנקודה החשודה.
- יש להציב שישה ערכי קרובים לתוצאה אותה קיבלנו לפני ואחרי הנקודה.
- לחשב את ערך ה- של ה- באמצעות הצבה בטבלה.
- לבחון את התנהגות הפונקציה:
- אם ערך ה- גדל ככל שמתקרבים לנקודה סימן שמדובר באסימפטוטה.
- אם ערך ה- קטן (כלומר מתכנס לנקודה) ככל שמתקרבים לנקודה סימן שמדובר בחור.
סיכום
אסימפטוטה - הפונקציה שואפת לאינסוף (או מינוס אינסוף). מתקבל בעקבות מספר המאפס את המכנה בלבד.
חור - נקודה בה הפונקציה לא עוברת. מתקבל בעקבות קיים מספר המאפס את המכנה אך לאחר הצבה במונה הוא שווה לאפס גם.