תורת החישוביות/כריעות שפות/שפות שאינן כריעות/ארגז חול

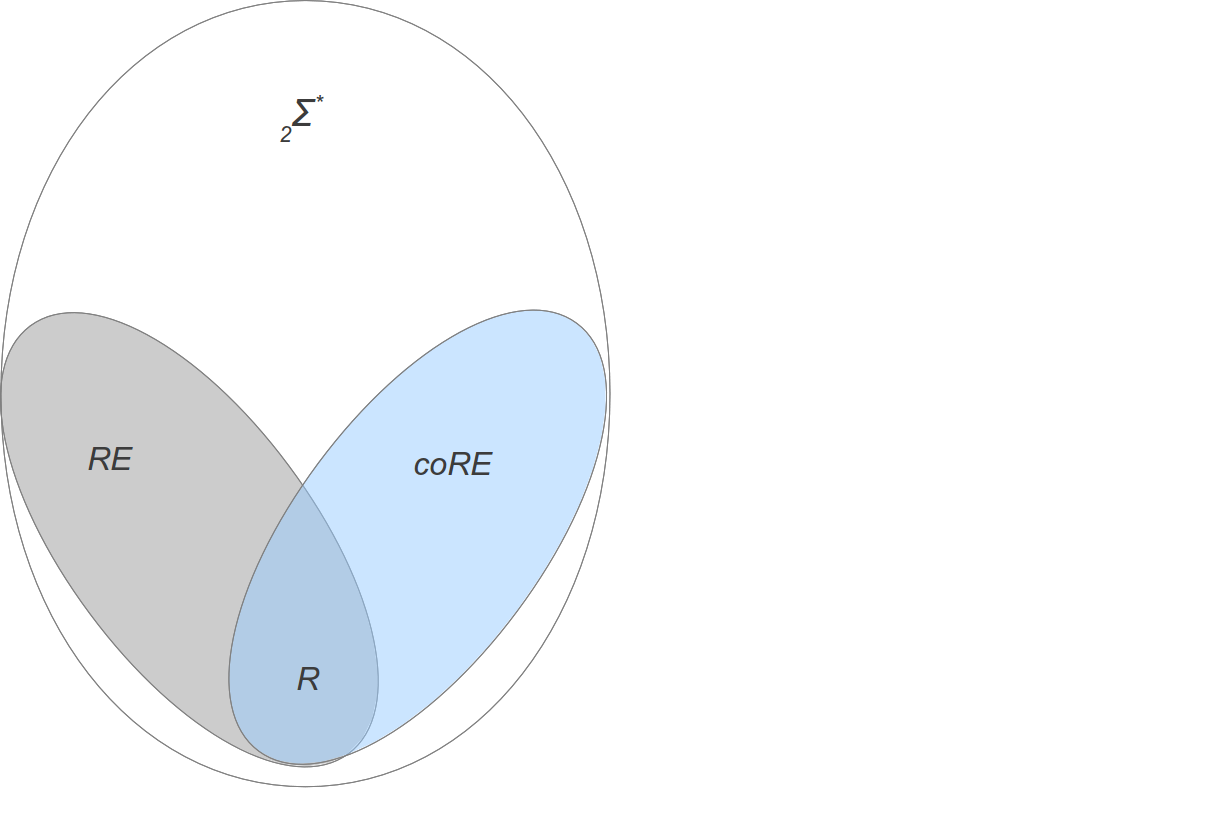
בחלקים הקודמים ראינו מספר קבוצות של שפות: R, RE, coRE, וכמובן, קבוצת העל $Σ^{*}$ . בחלק זה נראה ש"תמונת העולם" נראית כבתרשים הבא.

כלומר,

הקבוצה $Σ^{*} ∖ R E$ איננה ריקה

משיקולי מניה אפשר לראות שבהכרח יש שפות ב $Σ^{*} ∖ R E$ .

ראשית נראה שיש יותר שפות ממחרוזות. תבנית:טענה

בעזרת הטענה הקודמת, אפשר לראות שבהכרח ישנן שפות ב $Σ^{*} ∖ R E$ תבנית:הוכחה

בחלק קודם כבר ראינו מספר דוגמאות לשפות בRE: השפה האוניברסלית, שפת האלכסון, ובעיית העצירה. כעת נראה כי שפות אלו הן ב $R E ∖ R$ .

נניח, על דרך השלילה, שקיימת מ"ט כריעה, העונה על השאלה האם מ"ט M עוצרת על קלט x. נקרא למכונה זו H. כעת נבנה את המכונה $H^{'}$ באופן הבא:

בהנתן קידוד מ"ט M, המכונה קודם תריץ את $H (⟨ M ⟩, ⟨ M ⟩)$ , (נזכור שתמיד חלק זה עוצר, שכן הנחתנו בשלילה היא שהבעיה כריעה, וH מימוש שלה).
אם התשובה חיובית, אז $H^{'}$ תכנס ללולאה אינסופית. אחרת, היא תעצור.

כעת נקבל מצב אבסורד לגבי הריצה $H^{'} (⟨ H^{'} ⟩)$ :

אם היא עוצרת, אז בהכרח $H (⟨ H^{'} ⟩, ⟨ H^{'} ⟩)$ מחזירה תשובה שלילת (מפני שהיא השלב הראשון בריצת $H^{'}$ שכתוצאתו הוחלט לעצור). אבל לפי ההגדרה, משמעות תשובה שלילית זו היא ש $H^{'} (⟨ H^{'} ⟩)$ איננה עוצרת, ולכן יש סתירה.
אם היא איננה עוצרת, אז בהכרח $H (⟨ H^{'} ⟩, ⟨ H^{'} ⟩)$ מחזירה תשובה חיובית (שוב, מפני שהיא השלב הראשון בריצת $H^{'}$ שכתוצאתו הוחלט להכנס ללולאה אינסופית). אבל לפי ההגדרה, משמעות תשובה חיובית זאת היא ש $H^{'} (⟨ H^{'} ⟩)$ עוצרת, ולכן שוב יש סתירה.

נתבונן בשפה המשלימה לשפת האלכסון, כלומר

\overline{L_{D}} = {⟨ M ⟩ ∣ ⟨ M ⟩ \notin L (M)}

.

בחלק זה נשתמש בתכונות בסיסיות של רדוקציות ומשפטי רדוקציה כדי להראות שמספר שפות אינן כריעות.