אלגברה מופשטת על כוס קפה/רשימת מושגים1
רשימת מושגים חיוניים, והסבר של כל אחד מהם
עבור כל אחד מהמושגים הבאים, יובא:
- הסבר אינטואיטיבי.
- דוגמה או דוגמאות להמחשה.
- במידת הצורך: הוכחת המשפט.
קטגוריה
- קטגוריה - הערך מויקי האנגלית.
- תבנית:כ An Introduction to n-Categories.
הסבר כללי
- תבנית:כ A MERE SET.
- עצם מתמטי - הערך מויקי האנגלית.
- כל השרטוטים במקור זה נמצאים בדף: משתמש:Yoelpiccolo31/Yoelpiccolo31/מתמטיקה/שרטוטים ב- LATEX.
מהי n-category ?
n-category הנו סוג של מבנה אלגברי, המורכב מ:
- עצמים (אובייקטים) (ככל הנראה אבני הבסיסתבנית:הבהרה). אובייקט יכול להיות זהה לעצמו, תוך הצגתו בדרכים שונות. מכאן ניתן להסיק, כי יש לאובייקט חבורה סימטריתתבנית:הבהרה- חבורת האוטומורפיזמים שלותבנית:הבהרה.
- מורפיזמים בין עצמים (אובייקטים)- פעולות שונות שניתן לבצע בין אובייקטים שונים, והקשר בין אובייקטים אלו.
- מורפיזמים בין שני מורפיזמים ("2-morphisms")- פעולות שונות שניתן לבצע בין שני מבנים שונים, המכונים "מורפיזמים"- והקשר בין שני מבנים אלו.
- מורפיזמים בין n-morphisms - פעולות שונות שניתן לבצע בין n מבנים שונים, המכונים "מורפיזמים"- והקשר בין n מבנים אלו.
כל שלב מהווה "קופסה שחורה" של הסעיף הקודם, ומורכב מאברי הסעיף הקודם.
- 0-category הנו קבוצה.
- 1-category הנה קטגוריה. בקטגוריה מורפיזמים בקטגוריה עשויים להיות זהים זה לזה או שונים זה מזה. אין מושג המכונה: "מורפיזמים איזומורפיים".
ב- 2-category לא ניתן לדבר אודות 2-morphisms איזומורפיים. לשם כך, אנו צריכים לדעת פרטים אודות 3-category , וכן הלאה.
מושגים שונים של n-Category
על מנת להסביר את המושג של n-categories , נוח להשתמש באיורים.
- אנו מתייחסים לאובייקטים כ- 0-dimensional (בעלי ממד אפס), כלומר: נקודות.
- אנו מתייחסים למורפיזמים כ- 1-dimensional (בעלי ממד אחד), כלומר: אינטרוולים, או במדויק יותר: חיצים המקשרים בין נקודה אחת לרעותה.
באיור הבא, אנו מצרפים שתי העתקות שונות יחדיו- ליצירת העתקה חדשה:
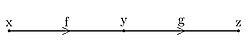
תבנית:שתבנית:שתבנית:שתבנית:שתבנית:שתבנית:שתבנית:ש

תבנית:שתבנית:שתבנית:שתבנית:שתבנית:שתבנית:שתבנית:שתבנית:שתבנית:ש
להסביר: isomorphism for equality, עבור n-categories, כאשר n הנו מספר גדול באופן שרירותי (גדול כרצוננו)תבנית:הבהרה.
כרגע, נסתפק בהבנה כללית (ה"מאקרו") של המושג, ללא פירוט מעמיק (ה"מיקרו") כיצד בנויים המורפיזמים, וכיצד הם מקושרים זה לזה.
כמו כן, נסקור מספר מושגים של n-category , בדגש על n-category "חלשות".
n-morphism מהווה יחס שקילות ("equivalence")תבנית:הערה אם הוא הפיך (" invertible"), בעוד ש j-morphism עבור j<n מהווה יחס שקילות, אם הוא הפיך עד j + 1)-morphism) המהווה יחס שקילות.
דיאגרמה (תורת הקטגוריות)
דיאגרמה (תורת הקטגוריות), תבנית:אנ.
הערה: לא כל דיאגרמה היא קומוטטיבית, כפי שמצוין בערך העברי.
מפה (מתמטיקה)
העתקה ליניארית
מורפיזם
הומומורפיזם
איזומורפיזם
איזומורפיזם של גרפים
אוטומורפיזם
משוואת "החלום של פרשמן"
הערך: "החלום של פרשמן (מתמטיקה)" ("Freshman's dream") תבנית:אנ.
קריטריון איזנשטיין
מה זה? למה צריך את זה? ובמה זה עוזר לנו/מקדם אותנו?
קריטריון אייזנשטיין מספק תנאי מספיק עבור פולינום בעל מקדמים, שהם מספרים שלמים- לכך שיהיה אי פריק מעל שדה המספרים הרציונליים.
פולינום אי פריק הנו פולינום אשר לא ניתן לכתבו כמכפלה של שני פולינומים כלשהם, שאינם קבועים, והם בעלי מקדמים רציונליים.
קריטריון זה אינו בר השמה עבור כל הפולינומים
הקריטריון
נניח שברשותנו הפולינום הבא, בעל מקדמים שהם מספרים שלמים:
.
אם קיים מספר ראשוני , המקיים את שלושת התנאים הבאים:
- מחלק כל , כך ש: , או, למעשה: .תבנית:שמשמעות הדבר היא, שעל לחלק את כל מקדמי הפולינום, מלבד המקדם של החזקה הגבוהה ביותר בו (או, במילים פשוטות: מלבד המקדם של סדר הפולינום).תבנית:שתבנית:ש
- לא מחלק את (כלומר, אינו מחלק את מקדם החזקה הגבוהה ביותר של הפולינום, או בפשטות: אינו מחלק את המקדם של סדר הפולינום).תבנית:שתבנית:ש
- לא מחלק את .
אזי הפולינום הנו אי פריק מעל שדה המספרים הרציונליים.
דוגמאות
ניתן להחיל את קריטריון אייזנשטיין באופן ישיר (כלומר, שימוש בפולינום המקורי), או לאחר טרנספורמציה (העתקה) של הפולינום המקורי.
- החלת קריטריון אייזנשטיין באופן ישיר (ללא טרנספורמציה (העתקה)):
נתון לנו הפולינום הבא:
.
על מנת להחיל את קריטריון אייזנשטיין על הפולינום הזה, עלינו לבחור מספר ראשוני , כך שיקיים שלושה תנאים:
- יחלק, ללא שארית, את שני המקדמים הלא מובילים שלו,תבנית:שדהיינו: אנו צריכים למצוא מספר ראשוני, כך שיחלק הן את והן את - ללא שארית.תבנית:שתבנית:שהמספר הראשוני היחיד, אשר עונה לדרישה הזו, הוא: .תבנית:שתבנית:שכלומר, מצאנו מספר ראשוני , אשר עונה על הדרישה הראשונה (מתוך שלוש). תבנית:בוצע
- לא מחלק את מקדם האיבר המוביל ללא שארית:תבנית:שתבנית:ש .תבנית:שתבנית:שכלומר, לאחר החילוק נותרה שארית. תבנית:בוצע
- ריבוע המספר הראשוני, , אינו מחלק את מקדם האיבר האחרון, , ללא שארית:תבנית:שתבנית:ש .תבנית:שתבנית:שכלומר, לאחר החילוק נותרה שארית. תבנית:בוצע
- החלת קריטריון אייזנשטיין באופן עקיף (לאחר טרנספורמציה (העתקה)):
לעתים קרובות, קריטריון אייזנשטיין אינו מתאים עבור כל מספר ראשוני . אולם, הוא כן עשוי להתאים עבור מספר ראשוני כלשהו, באם נבצע החלפה (או, ליתר דיוק, העתקה) של הפולינום המקורי, כך שנציב בו במקום כל אשר קיים בו. כך יתקבל פולינום חדש, אשר ניתן להחיל עליו את קריטריון אייזנשטיין (כלומר, הפולינום לאחר ביצוע ההעתקה הנו אי פריק).תבנית:שכמו כן, העובדה שהפולינום החדש, לאחר ההעתקה, הנו אי פריק- מאפשרת לנו להסיק, שהפולינום המקורי אף הוא אי פריק.
דוגמה:
נתון לנו הפולינום הבא:
, אשר מקדם ה- שלו שווה ; לפיכך, מקדם זה אינו ניתן לחלוקה על ידי אף מספר ראשוני ( איננו מספר ראשוני, רק מספרים השווים או הגדולים מ- ).תבנית:ש(תזכורת: על פי הקריטריון, על המספר הראשוני לחלק, ללא שארית, את שני המקדמים הלא מובילים שלו).תבנית:שמכאן נסיק, שלא ניתן להחיל על הפולינום את קריטריון אייזנשטיין.תבנית:שאבל, נוכל לעשות זאת באמצעות החלפת כל ה- ים בפולינום ב- - לקבלת פולינום חדש: .
כעת, קריטריון אייזנשטיין מתקיים, עבור: .
עצם העובדה שאנו מקבלים פולינום אי פריק לאחר ביצוע ההחלפה () - מעיד על כך שגם הפולינום המקורי, - הנו בלתי פריק.תבנית:שמסקנה זו נכונה, מאחר שההחלפה שביצענו מהווה אוטומורפיזם של החוג (למה?תבנית:הבהרה).
קריטריון האי פריקות של קון
משפט דיריכלה
משפט השאריות הסיני
המכנה המשותף המקסימלי ((Greatest common divisor (GCD)
אלגוריתם אוקלידס
נוסחת ההיפוך של מביוס
נוסחת ההיפוך של מביוס, תבנית:אנ.
קונבולוציה
יריעה
המשפט הקטן של פרמה
הומומורפיזם פרובניוס
הומומורפיזם פרובניוס, תבנית:אנ.
האוטומורפיזם של פרובניוס
הוכחת משפטים הקשורים לפרובניוס, כולל האוטומורפיזם של פרובניוס.