מתמטיקה תיכונית/גיאומטריה אוקלידית/משפטים בגאומטריה/ישרים/משפט תאלס

היחס בין שוקי הזווית

שני הישרים מאותו צד של הקדקוד

הקדקוד כלוא בין הישרים

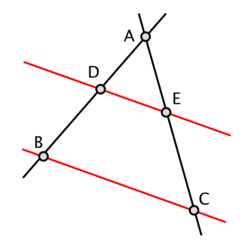
ניעזר בסימונים שבציור בצד.

נתון $BC||DE$ , צריך להוכיח $\frac{AB}{AD}=\frac{AC}{AE}$

נעביר את $BE$ ואת $CD$ .

נסתכל על המשולש $BDE$ ועל המשולש $CDE$ .

בשני משולשים אלו, $DE$ צלע, והגובה מ- $B$ ל- $DE$ שווה לגובה מ-$C$ ל- $DE$ . (כי $DE||BC$)

לכן, שטחי משולשים אלו שווים, כלומר $S_{\mathrm{△}BDE}=S_{\mathrm{△}CDE}$

אם הישרים מאותו צד של הקדקוד (הציור העליון), נוסיף לשני הצדדים את שטח המשולש $ADE$ .

אם הקדקוד כלוא בין הישרים (הציור התחתון), נוריד משני האגפים את שטח המשולש $ADE$ .

נקבל $S_{\mathrm{△}ABE}=S_{\mathrm{△}ACD}$

נחלק את שני האגפים בשטח המשולש $ADE$ , ונקבל $\frac{S_{\mathrm{△}ABE}}{S_{\mathrm{△}ADE}}=\frac{S_{\mathrm{△}ACD}}{S_{\mathrm{△}ADE}}$

נוריד גובה $h_1$ מ- $E$ ל- $AB$ , וגובה $h_2$ מ- $D$ ל- $AC$ .

מכיון ששטח משולש שווה למחצית מכפלת צלע בגובה לה, נקבל: $\frac{\frac{h_{1}AB}{2}}{\frac{h_{1}AD}{2}}=\frac{\frac{h_{2}AC}{2}}{\frac{h_{2}AE}{2}}$

לאחר צמצום, נקבל: $\frac{AB}{AD}=\frac{AC}{AE}$

היחס בין הישרים החותכים את הזווית

נסמן נקודה M על BC כך ש-$DM\Vert EC$

מכיון ש- $DM\Vert EC$ ו-$DE\Vert MC$, DECM [[/../../מקבילית|מקבילית]]

לכן, DE=CM

אם נסתכל על B כקדקוד, נקבל, ע"פ היחס בין שוקי הזווית (שהוכח לעיל): $\frac{BA}{AD}=\frac{BC}{CM}$

אם נציב DE=CM, נקבל: $\frac{BA}{AD}=\frac{BC}{DE}$

ע"פ כלל המעבר, נקבל: $\frac{AB}{AD}=\frac{AC}{AE}=\frac{BC}{DE}$