מבוא לשיטות נומריות/מציאת שורשים של משוואה

הקדמה:

• באמצעות איטרציות נרצה למצוא פתרון (שורשים) של משוואה.

• ההנחה: $f(x)$ - פונקציה רציפה.

מתי:

• כאשר הפתרון האנליטי לא קיים או קשה לחישוב.

• בעיות מינימום ומקסימום.

• כשלב בפתרון בעיות מורכבות יותר.

שיטות פתרון:

א) שיטות תחום:

1) חציית התחום.

2) אינטרפולציה לינארית.

ב) שיטות פתוחות:

1) ניוטון-רפסון.

2) חיתוך.

3) איטרציות רצופות.

א) שיטת תחום:

1) חציית התחום:

התקדמות על גרף הפונקציה עד מציאת שינוי סימן בין $[X_0,X_1]$. אז, בודקים את ערך הפונקציה במרכז $X_2=\frac{X_0+X_1}{2}$ והמשך צמצום המרווח פי 2 עד להגעה לפתרון הקרוב ביותר לפי הקירוב הרצוי.

• שלבי פתרון:

1) מנחשים 2 פתרונות התחלתיים כך שסימני $f(X_1),f(X_2)$ הפוכים.

2) מבצעים איטרציות עוקבות $X_{new}=\frac{x_1+x_2}{2}$

3) אם $f(x_{new})\cdot f(x_1)<0$ אז $X_2=X_{new}$

אם $f(x_{new})\cdot f(x_1)>0$ אז $X_1=X_{new}$

תיאור גרפי:

קובץ:Numeriot (4).png

תיאור גרפי

פתרון התחלתי: $f(X_1)<0,f(X_2)>0$

$X_3=\frac{X_1+X_2}{2},f(X_3)<0\Rightarrow [X_3,X_2]$

$X_4=\frac{X_3+X_2}{2},f(X_4)>0\Rightarrow [X_3,X_4]$

4) אם $f(X_{new})=0$ אז $X_{new}$ הוא הפתרון המבוקש ויש לעצור את האיטרציות.

התכנסות:

• ${ϵ}_n$ הוא השגיאה בכל איטרציה ${ϵ}^{(n)}<|X_2^{(n)}-X_1^{(n)}|$

• בכל איטרציה תחום הפתרון קטן בחצי ולכן ניתן לרשום: $\frac{|{ϵ}^{(n+1)}|}{|{ϵ}^{(n)}|}\cong \frac{1}{2}$

• מדובר בקצב התכנסות לינארי $k=\frac{1}{2},R=1$

• ניתן לדעת מראש את מספר האיטרציות הדרוש להשגת הדיוק הנדרש:

$|{ϵ}^{(n)}|\cong {\left(\frac{1}{2}\right)}^n|X_2^{(0)}-X_1^{(0)}|<\delta$

כאשר:

$\delta$ - הדיוק הנדרש מאיתנו

$|X_2^{(0)}-X_1^{(0)}|$ - גודל התחום הראשון

n - מספר האיטרציות

נחלץ את n (מספר האיטרציות):

$n>\frac{log(|X_2^{(0)}-X_1^{(0)}|)-log\delta }{log2}$

יתרונות השיטה:

• איטרציות פשוטות מאוד.
• מספר האיטרציות הדרוש ידוע מראש.
• התכנסות מכל פתרון התחלתי.
• מקבלים גבולות תחום לפתרון בכל איטרציה.

חסרונות השיטה:

• דרושים 2 פתרונות התחלתיים.
• ההתכנסות הלינארית איטית יחסית.
• אינו מנצל מידע על הפונקציה.

2) שיטת האינטרפולציה הלינארית

דומה לשיטת חציית התחום, השוני הוא באופן חישוב הנקודה החדשה $X_{new}$.

נבצע אינטרפולציה לינארית של 2 הפתרונות הנוכחיים, קירוב לינארי של f(X) וחיפוש השורש של הקירוב.

* משוואת הישר:

עבור 2 נקודות $(X_1,f(X_1)),(X_2,f(X_2))$ נרצה למצוא את הישר המחבר בינהן

$f(x)=ax+b$

$\{\begin{array}{c}f(X_1)=a{X}_1+b\\ f(X_2)=a{X}_2+b\end{array}\Rightarrow \{\begin{array}{c}a=\frac{f(X_1)-f(X_2)}{X_1-X_2}\\ b=\frac{f(X_2)\cdot X_1-f(X_1)\cdot X_2}{X_1-X_2}\end{array}$

$f(X_{new})=a{X}_{new}+b=0$

נקודת החיתוך של ישר זה עם ציר X:

$X_{new}=-\frac{b}{a}=\frac{f(X_2)\cdot X_1-f(X_1)\cdot X_2}{f(X_2)-f(X_1)}=X_1-\frac{X_2-X_1}{f(X_2)-f(X_1)}\cdot f(X_1)$

• האלגוריתם:

1) נמצא שני פתרונות התחלתיים $X_1^{(0)},X_2^{(0)}$ כך ש: $f(X_1^{(0)})\cdot f(X_2^{(0)})<0$

2) נחשב פתרון חדש (שהוא החיתוך עם ציר X של הישר המחבר בין 2 פתרונות התחלתיים אל:

$X_{new}=X_1-\frac{X_2-X_1}{f(X_2)-f(X_1)}\cdot f(X_1)$

3) נחשב את $f(X_{new})$

4) עדכון הפתרון:

• אם $f(X_{new})=0$ אז $X_{new}$ הוא הפתרון המבוקש.
• אם $f(X_{new})\cdot f(X_1^{(n)})>0$ אז $X_{new}=X_1^{(n+1)},X_2^{(n+1)}=X_2^{(n)}$
• אם $f(X_{new})\cdot f(X_1^{(n)})<0$ אז $X_1^{(n+1)}=X_1^{(n)},X_2^{(n+1)}=X_{new}$

• תיאור גרפי:

תיאור גרפי

• השיטה לא עובדת עבור פונקציות "שטוחות":

פונקציה שטוחה

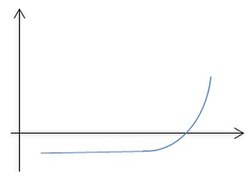
ההפרש בין $f(X_i)$ יהיה קטן, יתאים לתנאי $ϵ$ ויגרום למציאת פתרון שגוי.

התכנסות:

• עבור פונקציה קמורה/ קעורה ההתקדמות איטית.
• קצב ההתכנסות דומה לזה של שיטת חציית התחום.
• לא ניתן לקבוע מראש את מספר האיטרציות הדרוש להשגת דיוק נדרש.

ב) שיטות פתוחות

1) שיטת ניטון-רפסון:

• נעביר משיק לפונקציה בנקודה $x_0$ , $x_1$ תוגדר כנקודת חיתוך המשיק עם ציר x.

• נפתח ביטוי למשיק ע"י קירוב טיילור מסדר ראשון:

$\hat{f}(x)=f(x_0)+\frac{df(x_0)}{dx}(x-x_0)$ - קירוב למשיק

• נחשב את נקודת החיתוך עם ציר x של קירוב זה:

$f(x_0)+f^{\prime }(x_0)\cdot (x-x_0)=0$

$x=x_0-\frac{f(x_0)}{f^{\prime }(x_0)}$

• האיטרציה הכללית:

$x^{n+1}=x^n-\frac{f(x^{(n)})}{f^{\prime }(x^{(n)})}$

• תיאור גרפי:

קובץ:Numeriot (2).png

תיאור גרפי

• הפתרון עלול להתבדר כאשר הנגזרת הראשונה קרובה לאפס:

תיאור גרפי

• התכנסות:

${ϵ}^{(n+1)}=x^{(n+1)}-x^{*}=x^{(n)}-\frac{f(x^{(n)})}{f^{\prime }(x^{(n)})}-x^{*}={ϵ}^{(n)}-\frac{f(x^{(n)})}{f^{\prime }(x^{(n)})}$

כאשר:

$x^{*}$ - הוא הפתרון האמיתי - לא ידוע.

${ϵ}^{(n+1)}$ - השגיאה באיטרציה n+1.

• קצב ההתכנסות ריבועי (R=2)

${ϵ}^{(n+1)}\cong \frac{1}{2}\frac{f^{″}(x^{*})}{f^{\prime }(x^{*})}\cdot [{ϵ}^{(n)}{]}^2=O[|{ϵ}^{(n)}|{]}^2$

• הפתרון עלול לא להתכנס כאשר $f^{\prime }(x)\to 0$ בסביבת הפתרון.

2) שיטת החיתוך:

• בשיטת ניוטון-רפסון נאלצנו לחשב נגזרת - כעת נחפש קירוב אחר לביטוי השיפוע.

• נשתמש בשני הפתרונות האחרונים שחושבו ונמתח בינהם מיתר.

שיפוע המיתר: $f^{\prime }(x^{(n)})=\frac{f(x^{(n)})-f(x^{(n-1)})}{x^{(n)}-x^{(n-1)}}$

• נציב ביטוי זה באיטרציה הכללית של ניוטון-רפסון:

$x^{(n+1)}=x^{(n)}-\frac{x^{(n)}-x^{(n-1)}}{f(x^{(n)})-f(x^{(n-1)})}$

  $x^{(n+1)}=x^{(n)}-\frac{x^{(n)}-x^{(n-1)}}{f(x^{(n)})-f(x^{(n-1)})}\cdot f(x^{(n)})$

• משתמשים בשני הפתרונות האחרונים ולא בקצוות התחום.

• מדובר בביטוי זהה כמו בשיטת האינטרפולציה הלינארית: מחושב שיפוע המיתר במקום שיפוע המשיק.

• תיאור גרפי:

קובץ:Numeriot (3).png

תיאור גרפי

• בדומה לשיטת ניוטון-רפסון הפתרון עלול להתבדר:

קובץ:Numeriot (6).png

תיאור גרפי

• התכנסות: נפתח ביטוי לשגיאה עבור האיטרציה ה- n+1 (בדומה לשיטת ניוטון-רפסון): ${ϵ}^{(n+1)}=x^{(n+1)}-x^{*}$

כאשר:

$x^{*}$ - הפתרון האמיתי והלא ידוע.

${ϵ}^{(n+1)}$ - הגדרת השגיאה.

• קצב ההתכנסות:

${ϵ}^{(n+1)}\approx {(\frac{1}{2}\cdot \frac{f^{″}(x^{*})}{f^{\prime }(x^{*})})}^{0.618}\cdot [{ϵ}^{[n]}{]}^{1.618}=O[|{ϵ}^{(n)}{|}^{1.618}]$

• R > 1 : מדובר בהתכנסות סופר-לינארית.

• אם $1>>|f(x_n)-f(x_{n-1})|$ אז השיטה קורסת.

3) שיטת האיטרציות הרצופות - משמשת לבעיות מסובכות במיוחד.

• נגדיר פונקציה חדשה $x=g(x)$ שתהיה טרנספורמציה לבעיה הנתונה $f(x)=0$.

• ניתן לבצע את הטרנספורמציה בדרכים רבות:

$f(x)=x^3+x=0$

$\to g(x)=x^3+x+x=x$

• האיטרציה תבוצע לפי המשוואה:

$x_{(n+1)}=g(x_{(n)})$

• תיאור גרפי:

קובץ:Numeriot (8).png

תיאור גרפי

• שלבי הפתרון:

1) נמצא פתרון התחלתי $x^{(0)}$

2) עדכון הפתרון: $x^{(n+1)}=g(x^{(n)})$

• ההתכנסות של השיטה לינארית רק כאשר $|g^{\prime }(x^{*})|<1$ - תנאי להתכנסות

• ${ϵ}^{(n+1)}=x^{(n+1)}-x^{*}=g(x^{(n)})-x^{*}$ - השגיאה באיטרציה ה- n+1