מבני נתונים ואלגוריתמים - מחברת קורס/אלגוריתמים/סדרי גדילה

דף זה עוסק בסווג פונקציות (מתמטיות) ל"משפחות". כבר ראינו שלפעמים אפשר לקבוע חד-משמעית שאלגוריתם אחד פועל יותר טוב מאחר (עבור קלטים מספיק גדולים), על ידי סווגם למשפחות. אנו נתעניין בהגדרות מדוייקות לסיווגים גמישים יחסית, כמו "משפחת הפונקציות שגדלה כמו פונקציה לינארית", או "משפחת הפונקציות שגדלה יותר מהר מפונקציה לוגריתמית".

תבנית:הארה

הפונקציות בהן נעסוק

לרוב נעסוק בפונקציות המתארות את זמן הריצה של אלגוריתם (או חלק מאלגוריתם). לכן נתמקד בפונקציות מהצורה $f(n)$ בעלות המאפיינים הבאים:

• תחום ההגדרה חיובי שלם: $f(n)$ מוגדרת עבור ערכי $n$ שלמים חיוביים. תחום ההגדרה מציין את גודל הקלט.
• ערך חיובי וסופי: לכל $n$ חיובי ושלם, $0<f(n)<\mathrm{\infty }$. עבור גודל קלט כלשהו, זמן הריצה הוא חיובי ממש וסופי (נזכר שאלגוריתם פועל בזמן סופי עבור קלט בגודל סופי).
• מונוטוניות לא יורדת: $n>m\Rightarrow f(n)\ge f(m)$. נטפל בבעיות שעבורן "יותר קשה" לפתור בעיות גדולות מבעיות קטנות.

קבוצות סדרי הגדילה

הקבוצה $O$

הקבוצה $O(g(n))$ הנה קבוצת כל הפונקציות $f(n)$ כך ש$f(n)$, עבור $n$ גדול מספיק, חסומה מלמעלה ע"י $c\cdot g(n)$ עבור $c>0$ כלשהו. תבנית:מבנה תבנית

אינטואיציה לאו.

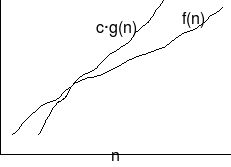
למרבה הצער, הסימון $O(g(n))$ משמש לשני דברים שונים: הקבוצה $O(g(n))$, או איבר מהקבוצה $O(g(n))$. שלוש הדוגמאות שראינו מסומנות בד"כ כ$n=O(n)$, ‏$n+3=O(n/2)$, ו$n^2\ne O(n)$.

תבנית:מבנה תבנית

הקבוצה $\mathrm{\Omega }$

הקבוצה $\mathrm{\Omega }(g(n))$ הנה קבוצת כל הפונקציות $f(n)$ כך שכל פונקציה $f(n)$, עבור $n$ גדול מספיק, חסומה מלמטה ע"י $c\cdot g(n)$, עבור $c>0$ כלשהו. תבנית:מבנה תבנית

אינטואיציה לאומגה.

תבנית:מבנה תבנית

בדיוק כמו ב$O(g(n))$, גם $\mathrm{\Omega }(g(n))$ משמשת לשני דברים: הקבוצה $\mathrm{\Omega }(g(n))$, או איבר הקבוצה $\mathrm{\Omega }(g(n))$. שלוש הדוגמאות הקודמות נכתבות בד"כ כ$n=\mathrm{\Omega }(n)$,‏ $n+3=\mathrm{\Omega }(n/2)$, ‏ ו$n^2=\mathrm{\Omega }(n)$.

תבנית:מבנה תבנית

הקבוצה $\mathrm{\Theta }$

הקבוצה $\mathrm{\Theta }(g(n))$ הנה החיתוך של$O(g(n))$ ו$\mathrm{\Omega }(g(n))$. תבנית:מבנה תבנית

אינטואיציה לתטא.

תבנית:שימו לב

תבנית:מבנה תבנית

תבנית:הארה

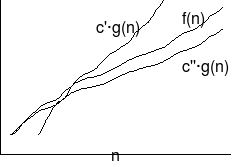
כללי סדרי גדילה

רפלקסיביות

תבנית:משפט (כבר הוכחנו זאת.)

דמיון לאופרטורי השוואה

בדף זה ראינו דרכים לסווג פונקציות לפי סדרי הגדילה שלהן. יש דמיון כלשהו בין הקבוצות שראינו לבין אופרטורי השוואה אלגבריים.

הקבוצה $O$ והייחס $\le$

הקביעה $f(n)\le g(n)$ אומרת ש$f(n)$ חסומה מלמעלה על ידי $g(n)$. הקביעה $f(n)=O(g(n))$ אומרת שקצב הגדילה של$f(n)$ חסום מלמעלה על ידי קצב הגידול של $g(n)$. יש דמיון כלשהו בין שתי הקביעות.

ראשית, נשים לב שמתקיים $f(n)\le g(n)\Rightarrow f(n)=O(g(n))$ (למה?).

יש עוד נקודות דמיון. בין היתר:

• רפלקסיביות: לכל פונקציה $f(n)$ מתקיים $f(n)\le f(n)$, ובאותו אופן, מתקיים $f(n)=O(f(n))$.
• טרנזיטיביות: לכל $f(n),g(n),h(n)$ מתקיים $f(n)\le g(n)\bigwedge g(n)\le h(n)\Rightarrow f(n)\le h(n)$ ,ובאותו אופן, $f(n)=O(g(n))\bigwedge g(n)=O(h(n))\Rightarrow f(n)=O(h(n))$

הקבוצה $\mathrm{\Omega }$ והייחס $\ge$

הקביעה $f(n)\ge g(n)$ אומרת ש$f(n)$ חסומה מלמטה על ידי $g(n)$. הקביעה $f(n)=\mathrm{\Omega }(g(n))$ אומרת שקצב הגדילה של$f(n)$ חסום מלמטה על ידי קצב הגידול של $g(n)$. יש דמיון כלשהו בין שתי הקביעות.

ראשית, נשים לב שמתקיים $f(n)\ge g(n)\Rightarrow f(n)=\mathrm{\Omega }(g(n))$ (למה?).

יש עוד נקודות דמיון. בין היתר:

• רפלקסיביות: לכל פונקציה $f(n)$ מתקיים $f(n)\ge f(n)$, ובאותו אופן, מתקיים $f(n)=\mathrm{\Omega }(f(n))$.
• טרנזיטיביות: לכל $f(n),g(n),h(n)$ מתקיים $f(n)\ge g(n)\bigwedge g(n)\ge h(n)\Rightarrow f(n)\ge h(n)$ ,ובאותו אופן, $f(n)=\mathrm{\Omega }(g(n))\bigwedge g(n)=\mathrm{\Omega }(h(n))\Rightarrow f(n)=\mathrm{\Omega }(h(n))$

הקבוצה $\mathrm{\Theta }$ והייחס $=$

הקביעה $f(n)=g(n)$ אומרת ש$f(n)$ שווה ל$g(n)$. הקביעה $f(n)=\mathrm{\Theta }(g(n))$ אומרת שקצב הגדילה של$f(n)$ שווה לקצב הגידול של $g(n)$. יש דמיון כלשהו בין שתי הקביעות.

ראשית, נשים לב שמתקיים $f(n)=g(n)\Rightarrow f(n)=\mathrm{\Theta }(g(n))$ (למה?).

יש עוד נקודות דמיון. בין היתר:

• רפלקסיביות: לכל פונקציה $f(n)$ מתקיים $f(n)=f(n)$, ובאותו אופן, מתקיים $f(n)=\mathrm{\Theta }(f(n))$.
• טרנזיטיביות: לכל $f(n),g(n),h(n)$ מתקיים $f(n)=g(n)\bigwedge g(n)=h(n)\Rightarrow f(n)=h(n)$ ,ובאותו אופן, $f(n)=\mathrm{\Theta }(g(n))\bigwedge g(n)=\mathrm{\Theta }(h(n))\Rightarrow f(n)=\mathrm{\Theta }(h(n))$.

עוד נקודות דמיון

יש עוד נקודות דמיון, לדוגמה:

1. סימטריה הופכית: לכל שתי פונקציות $f(n),g(n)$,‏ $f(n)\le g(n)\iff g(n)\ge f(n)$, ובאותו אופן, $f(n)=O(g(n))\iff g(n)=\mathrm{\Omega }(f(n))$.
2. לכל שתי פונקציות $f(n),g(n)$,‏ $f(n)=g(n)\iff f(n)\le g(n)\bigwedge f(n)\ge g(n)$, ובאותו אופן, $f(n)=\mathrm{\Theta }(g(n))\iff f(n)=O(g(n))\bigwedge f(n)=\mathrm{\Omega }(g(n))$.

מגבלות הדמיון

לדמיון בין הקבוצות לאופרטורים שראינו יש גם מגבלות. בין היתר:

1. לא תמיד נכון ש$2\cdot f(n)\le f(n)$, אך תמיד נכון ש$2\cdot f(n)=O(f(n))$.
2. תמיד מתקיים ש$f(n)\le g(n)\Rightarrow 2^{f(n)}\le 2^{g(n)}$, אך לא תמיד מתקיים $f(n)=O(g(n))\Rightarrow 2^{f(n)}=O(2^{g(n)})$.

דוגמה לשילוב מספר כללים

נפשט את הביטוי $f(n)=\sum _{i=1}^n[\mathrm{\Theta }(1)+\mathrm{\Theta }(i)]$.

ראשית, נשים לב ש $\mathrm{\Theta }(1)+\mathrm{\Theta }(i)=\mathrm{\Theta }(i+1)$ מכלל האדיטיביות. אבל $\mathrm{\Theta }(i+1)=\mathrm{\Theta }(i)$, מפני ששני הביטויים בתוך ה$\mathrm{\Theta }$ הם פולינומים ב$i$ בעלי דרגה 1. לכן נקבל $f(n)=\sum _{i=1}^n[\mathrm{\Theta }(i)]$.

כעת נשתמש שוב באדיטיבות:

$f(n)=$
$\sum _{i=1}^n[\mathrm{\Theta }(i)]=$
$\mathrm{\Theta }(1)+\mathrm{\Theta }(2)+\cdots +\mathrm{\Theta }(n)=$
$\mathrm{\Theta }(1+2+\cdots +n=$
$\mathrm{\Theta }(\sum _{i=1}^n[i])$

אבל $\sum _{i=1}^n[i]=\frac{n(n+1)}{2}$, מפני שזה טור חשבוני פשוט. לכן נקבל $f(n)=\mathrm{\Theta }\left(\frac{n(n+1)}{2}\right)$. כלומר, $\mathrm{\Theta }$ של פולינום ב$n$ בעל דרגה 2. לסיכום, לכן, נקבל $f(n)=\mathrm{\Theta }(n^2)$.

סיכום

בחיפוש לינארי ובינרי ראינו דוגמות ראשונות של ניתוח אלגוריתמים. דף זה עסק בסדרי גדילה של פונקציות.

בהנתן אלגוריתם כלשהו, נוכל לשאול לגביו מספר שאלות, לדוגמה:

1. מהו זמן הריצה של האלגוריתם במקרה הטוב ביותר?
2. מהו זמן הריצה של האלגוריתם במקרה הגרוע ביותר?
3. מהו זמן הריצה של האלגוריתם במקרה הממוצע? (לא נעסוק בכך בקורס זה, עם זאת).

לעתים נוכל לשאול שאלות מפורטות יותר אפילו:

1. מהו זמן הריצה הטוב ביותר של חיפוש בינרי בהנחה שהאיבר נמצא במערך?
2. מהו זמן הריצה הגרוע ביותר של חיפוש לינארי בהנחה שהאיבר אינו נמצא במערך?

בכל פעם שאנו מקבלים אלגוריתם ושאלה מסוג זה, התשובה הינה פונקציה (מתמטית) של $n$, גודל הקלט. נוכל להשתמש בקבוצות סדרי הגדילה שראינו כאן כדי לסווג את הפונקציה (המתמטית). כך לדוגמה, נוכל להגיד על אלגוריתם כלשהו "הוא פועל במקרה הגרוע ביותר בערך כמו פונקציה לינארית", או "הוא פועל במקרה הטוב ביותר פחות מאיזושהי פונקציה שורשית".