מתמטיקה תיכונית/גיאומטריה אוקלידית/משיק למעגל

להלן משפטים הקשורים במשיק למעגל.

משיק למעגל מאונך לרדיוס בנקודת ההשקה

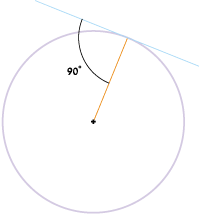
נתונים

מעגל וישר $L$ כלשהו שמשיק לו. (אפשר לשרטט לבד - ההוכחה לא דורשת בניות עזר מיוחדות).

הוכחה

נתבונן על סדרת המרחקים ממרכז המעגל לנקודה כלשהי על הישר. נתעלם לרגע מקיומו של המעגל ונתייחס למרכז המעגל כאל נקודה רגילה. אם כך, המרחק הקצר ביותר מאותה נקודה לישר הוא אורך האנך שיורד מהנקודה אל הישר. משום שהמשיק עובר דרך המעגל, גודלו של המרחק הזה הוא רדיוס המעגל - כלומר, קיבלנו שהרדיוס מאונך למשיק בנקודת ההשקה. מש"ל.

ישר המאונך לרדיוס בקצהו משיק למעגל

נתונים

1) $AO$ רדיוס

2) $A$ נקודת החיבור של הרדיוס עם הישר $L$

3) $L\perp AO$

הוכחה

4) נניח בשלילה $L$ אינו משיק למעגל.

5) $L$ חותך את המעגל בנקודה נוספת $B$ . (ישר החותך את המעגל ואינו משיק לו חותך אותו בשתי נקודות, לפי 2,4)

6) ב.ע. $BO$ רדיוס לנקודת החיתוך הנוספת.

7) $BO=AO$ (כל הרדיוסים שווים במעגל, לפי 1,6)

8) $\measuredangle OBA=\measuredangle OAB=90^{\circ }$ (זווית הבסיס שוות במשולש שווה שוקיים, לפי 3,7)

9) קיבלנו סתירה (סכום הזויות ב- $\mathrm{△}ABO$ גדול מ-180, לפי 8).

שני משיקים למעגל היוצאים מאותה נקודה שווים זה לזה עד לנקודת ההשקה

נתונים

1) $AB,AC$ משיקים למעגל שמרכזו $O$

הוכחה

2) ב.ע. $OB,OC$ רדיוסים לנקודות ההשקה.

3) ב.ע. $OA$ ישר העובר במרכז המעגל ובנקודת חיתוך המשיקים

4) $\measuredangle OBA=\measuredangle OCA=90$ (משיק למעגל מאונך לרדיוס בנקודת ההשקה)

5) $OA=OA$ (שוויון הינו רפלקסיבי - כל דבר שווה לעצמו)

6) $OB=OC$ (כל הרדיוסים שווים במעגל)

7) $\mathrm{△}OCA\cong \mathrm{△}OBA$ (מ-1,3,4 משפט חפיפה רביעי - צ.צ.ז)

8) $AB=AC$ (צלעות מתאימות במשולשים חופפים - נובע מ7)

קטע העובר במרכז המעגל ובנקודת חיתוך שני משיקים חוצה את הזוית שביניהם

נתונים

1) $AB,AC$ משיקים למעגל שמרכזו O

הוכחה

2) ב.ע. OB, OC רדיוסים לנקודות ההשקה.

3) $OA=OA$ (שוויון הינו רפלקסיבי - כל דבר שווה לעצמו)

4) $OB=OC$ (כל הרדיוסים שווים במעגל)

5) $AB=AC$ (כתוצאה מהמשפט הקודם)

6) $\mathrm{△}OCA\cong \mathrm{△}OBA$ (מ-3,4,5 משפט חפיפה ראשון - צ.צ.צ)

7) $\measuredangle OAB=\mathrm{\angle }OAC$ (זויות מתאימות במשולשים חופפים - נובע מ-6)

זוית בין משיק למיתר הנחתכים בנקודת ההשקה שווה לזוית ההקפית הנשענת על המיתר מצדו השני

שרטוט זמני

נתונים

שרטט מעגל שמרכזו בנקודה $O$ .

שרטט משולש $ABC$ במעגל.

שרטט משיק $AD$ למעגל בנקודה $A$ .

צ"ל:

$\measuredangle CAD=\measuredangle ABC$

הוכחה

---

שני מיתרים במעגל נחתכים כך שמכפלת קטעי האחד שווה למכפלת קטעי האחר

נתונים - 1) AB וCD מיתרים במעגל הנחתכים בנקודה E

הוכחה -

2) $\mathrm{\angle }DBA=\mathrm{\angle }DCA$ (שתי זוויות היקפיות הנשענות על אותה קשת שוות זו לזו)

3) $\mathrm{\angle }DEB=\mathrm{\angle }AEC$ (זוויות קודקודיות שוות זו לזו)

4) $\mathrm{\Delta }DEB\mathrm{\Delta }AEC$ (מ2,3 משפט דמיון שני ז.ז)

5) $DE*EC=EB*AE⟺\frac{DE}{AE}=\frac{EB}{EC}$ (צלעות מתאימות במשולשים דומים)

---

אם מנקודה מחוץ למעגל יוצאים שני חותכים למעגל אז מכפלת החלק החיצוני של כל חותך בחותך עצמו, שווה בשני החותכים

נתונים - ab חותך למעגל בנקודה d,תבנית:ש ac חותך למעגל בנקודה e.תבנית:ש צ"ל: ad*ab=ae*ac

הוכחה -תבנית:ש ב"ע: cb, de (מיתרים במעגל).תבנית:ש נתבונן במשולשים: abc, ade.

1. זווית a משותפת לשני המשולשים.
2. זווית bce, וזווית bde, שוות ל180 מעלות (זויות נגדיות במרובע חסום במעגל).
3. זויות ade=bce.
4. משולשים abc, aed דומים (מ1 ו3).
5. יחס הדמיון: ab/ae=ac/ad.
6. נכפול בהצלבה ונקבל: ab*ad=ac*ae

מש"ל.

---

אם מנקודה מחוץ למעגל יוצאים חותך ומשיק אז מכפלת החותך בחלקו החיצוני שווה לריבוע המשיק

נתונים - ab משיק למעגל בנקודה b.

ac חותך את המעגל בנקודות c, d.

צ"ל: ab*ab=ac*ad.

הוכחה - ב"ע: bc, bd מיתרים במעגל. נתבונן במשולשים abc, adb

1. זווית a משותפת לשני המשולשים.

2. זויות abd=c, (זווית בין משיק למיתר שווה לזווית ההיקפית הנשענת על אותו מיתר מצידו השני).

3. משולשים abc, adb דומים (מ1 ו2).

4. יחס הדמיון: