מתמטיקה תיכונית/טריגונומטריה/משפט הסינוסים

משפט הסינוסים

משפט הסינוסים מבטא את היחס בין צלע חלקי זווית הסינוס מולה ליחסה אל רדיוס של מעגל החוסם את המשולש. לפיה היחסים בין הצלעות, הזוויות והרדיוס:

$\frac{a}{\sin \alpha }=\frac{b}{\sin \beta }=\frac{c}{\sin \gamma }=2R$

שימושים:

1. בהינתן שתי זוויות וצלע אחת במשולש נקבל פתרון יחיד
2. בהינתן שתי צלעות וזוית מול אחתן מהן יתכן מצב בו נקבל שתי פתרונות אם הזווית הנתונה היא מול הצלע הקטנה.

הוכחה

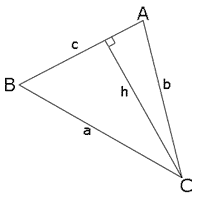
יחסי זוויות וצלעות

בהינתן משולש $\mathrm{△}ABC$ נוריד גובה מ-$C$ אל צלע $BA=c$.

משולש $\mathrm{△}DCA$ הוא ישר זווית (הורדנו גובה) ועל פי נוסחת הסינוס נוכל לטעון כי $sin\alpha =\frac{h}{b}$ דהינו $h=b*sin\alpha$

משולש $\mathrm{△}DCB$ הוא ישר זווית (הורדנו גובה) ועל פי נוסחת הסינוס נוכל לטעון כי $sin\beta =\frac{h}{a}$ דהינו $h=a*sin\beta$

נמצא את גובה המשולש באמצעות השווה של שתי המשוואות: $b*sin\alpha =a*sin\beta$

נעביר אגפים ונקבל $\frac{a}{\sin \alpha }=\frac{b}{\sin \beta }$.

באופן דומה נוכל להגיע למסקנה כי $\frac{a}{\sin \alpha }=\frac{b}{\sin \beta }=\frac{c}{\sin \gamma }$

הנוסחה נכונה עבור משולש חד זוויות. במידה והמשולש קהה זווית, ההוכחה נכונה עבור הזווית המשלימה של הזווית החדה. מצד שני על פי הזהות $\sin \alpha =\sin (180-\alpha )$ ולכן נוסחת הסינוסים נכונה עבור כלל המשולשים.

יחסי זוויות, צלעות וקוטר המעגל

אם מרכז המעגל החוסם הוא $O$, נמשיך את $BO$ עד שהוא נפגש עם המעגל ונקרא לנקודת החיתוך $D$.

נתבונן במשולש $\mathrm{△}BDC$.

הזווית $\mathrm{\angle }DCB=90^{\circ }$ (זווית ההיקפית הנשענת על קוטרו של המעגל).

בכדי להקל על החישוב נסמן ב -$\delta$ את הזווית $\mathrm{\angle }CDB$. כמו גם את הצלע $BC=a$ ו-$BD=2R$

על פי נוסחת הסינוס: $a=2R\sin \delta$

זווית $\delta$ שווה לזווית $\alpha$ כי הן נשענות על אותה קשת ולכן $a=2R\sin \alpha$

נעביר אגפים ונקבל $\frac{a}{\sin \alpha }=2R$