תורת החישוביות/סיבוכיות קולמוגורוב/יישומי אי-דחיסות

כי שראינו, אי אפשר לחשב את סיבוכיות הקולמוגורוב של סדרה ספיציפית כלשהי. מצד שני, ראינו בתת-הפרק אי דחיסות שתי תכונות מעניינות שלה:

1. לכל אורך סדרה נתון, ישנה סדרה לא דחיסה באורך זה.
2. רוב הסדרות אינן דחיסות בצורה משמעותית.

אלו אמירות חזקות מבחינה קומבינטורית, ובפרק זה נראה מספר יישומים שלהם. ביישום: חסמים תחתונים לסיבוכיות אלגוריתמים נראה יישום למציאת חסמים תחתונים לסיבוכיות אלגוריתמים, וביישום: אורך רצפים בסדרות בינאריות רנדומיות נראה יישום למציאת אורך הרצפים הצפויים בסדרה רנדומית.

יישום: חסמים תחתונים לסיבוכיות אלגוריתמים

אי-דחיסות מחרוזות משמש לעתים להוכחת חסמים תחתונים על זמני הריצה של סיבוכיות אלגוריתמים. הרעיון הכללי הוא כזה. בהנתן קלט $x$ כלשהו, מראים שאלגוריתם "יעיל מדי" הפועל עליו, מניב תיאור קצר במיוחד שלו, בסתירה לכך שלכל אורך נתון, יש לפחות מחרוזת אחת בלתי דחיסה לחלוטין.

שימוש להוכחת חסם תחתון על סיבוכיות מציאת פלינדרום

בעזרת סיבוכיות קולמוגורוב, אפשר להראות שסיבוכיות הכרעה האם מחרוזת היא פלינדרום ע"י מ"ט בעלת סרט יחיד היא לפחות ריבועית באורך הקלט.

נניח שקיימת מ"ט $M$ המצליחה להכריע האם קלט הוא פלינדרום. נתן לה את הקלט $x{0}^n{x}^r$ כאשר:

1. $x$ היא מחרוזת באורך $n$.
2. $0^n$ היא רצף של $n$ אפסים.
3. $x^r$ היא המחרוזת $x$ בהיפוך.

היות שמדובר בפלינדרום, $M$ חייבת לזהותו ככזה.

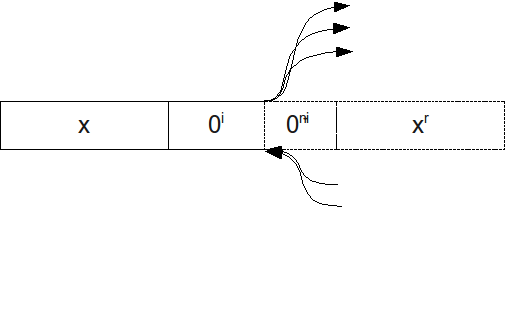
כל תו במחרוזת רשום בתא, ויש גבול בינו לבין התא שמימינו. במהלך ריצת האלגוריתם, חוצה ראש המכונה גבול זה מספר פעמים (החציות האי-זוגיות הן לכוון ימין, והאי זוגיות לכוון שמאל). בכל פעם שנחצה הגבול, $M$ נמצאת במצב מסויים. נסמן ב$C(i)$ את סדרת המצבים של החציות של תא $i$. בפרט נתמקד בסדרות החציות של התווים בחלק האמצעי של המחרוזת (החלק המורכב כולו מאפסים, כלומר $n\le i\le 2n$).

נניח שזמן ריצת האלגוריתם הוא $t(n)$. בהכרח, סך כל החציות, ובפרט סך כל החציות בתוך החלק האמצעי, הוא $t(n)$ גם כן. מעקרון שובך היונים נובע שקיים $i$ כלשהו בחלק האמצעי (כלומר $n\le i\le 2n$) שעבורו $|C(i)|\le \frac{t(n)}{n}$. כעת נראה שאפשר לתאר את $x$ לחלוטין ע"י השלשה המורכבת מ:

1. המספר $n$
2. המספר $i$
3. הסדרה $C(i)$

נעשה זאת בעזרת מכונה המקבלת את השלשה הנ"ל, ובנתן מחרוזת כלשהי, מסמלצת את פעולת $M$ באופן הבא.

נניח שנתנת המחרוזת כלשהי. אם אורך המחרוזת אינו $n$, המכונה עוצרת. אם כן, המכונה רושמת את המחרוזת, לאחריה $i$ אפסים ומתחילה לסמלץ את $M$. הסמלוץ מתחיל כמובן כאשר ראש $M$ בתא השמאלי ביותר. בכל פעם שנחצה הגבול $i$ לכוון ימין, המכונה המסמלצת בודקת האם מצב $M$ הוא זה שרשום ב$C(i)$: אם לא, היא דוחה את המחרוזת, ואם כן, היא ממשיכה את הסימולציה בחצייה לכוון שמאל במצב הבא. אם לא נותרו מעברים ימינה, המכונה המסמלצת תקבל.

אם כך קבלנו שמתקיים $K(x)\le {\log }_{|\mathrm{\Sigma }|}(n)+{\log }_{|\mathrm{\Sigma }|}(i)+c\frac{t(n)}{n}$ מצד שני ממשפט: קיום מחרוזות אי-דחיסות שראינו מקודם, בהכרח קיים $x$ שעבורו $K(x)\ge |x|=3n$ משילוב שני האי-שוויונים, נקבל $t(n)=\mathrm{\Omega }\left(n^2\right)$.

חסם תחתון על סיבוכיות מיון מבוסס השוואות

בעזרת סיבוכיות קולמוגורוב אפשר להראות חסם תחתון על מיון מבוסס השוואות. הרעיון הוא שמיון יעיל מדי היה מוצא דרך לדחוס פרמוטציות מעבר למה שאפשרי קומבינטורית.

יישום: אורך רצפים בסדרות בינאריות רנדומיות

נניח מחרוזת בינרית $x$ שאורכה הוא $n=|x|$. מה אורכי הרצפים של אפסים ואחדות שאפשר לצפות למצוא במחרוזת? נשתמש במשפט: אי-דחיסות משמעותית של רוב המחרוזות שראינו לעיל, לפיו רוב המחרוזות אינן דחיסות ביותר מ-$p$ קבוע כלשהו, כדי לענות על כך. מספיק שנוכיח שתכונה נובעת מכך שמחרוזת איננה דחיסה ביותר מ-$p$, כדי שהדבר יהיה נכון לרוב המחרוזות. כזכור 99.9% מהמחרוזות אינן דחיסות ביותר מ10 תווים.

מחרוזת רנדומית, לכן, כנראה לא תכיל רצפים ארוכים מדי. מצד שני, היא גם לא תכיל רק רצפים קצרים מאד - גם זו תכונה שמקנה מבנה דחיס למחרוזת. תבנית:משפט